El Triángulo de Pascal o Triángulo de Tartaglia es una disposición de números en forma triangular que se utiliza en matemáticas para resolver problemas relacionados con combinaciones, permutaciones y coeficientes binomiales. Este triángulo fue descubierto en el siglo XVII por el matemático italiano Niccolò Fontana Tartaglia y.. La fórmula general del binomio de Newton es la siguiente: donde. Solo recordar que n! , k! y ( n – k )! son factoriales. Por ejemplo: Pues bien, resulta que cada fila del triángulo de Pascal corresponde a los coeficientes del desarrollo de la potencia respectiva del binomio de Newton: Y esto es verdaderamente útil, pues es uno de los.

Triángulo de pascal ejercicios YouTube

Triángulo de Pascal Física y matemáticas Matemáticas

PPT Guía 8 El Triángulo de Pascal PowerPoint Presentation, free download ID3320722

Triangulo de pascal ejercicios resueltos YouTube
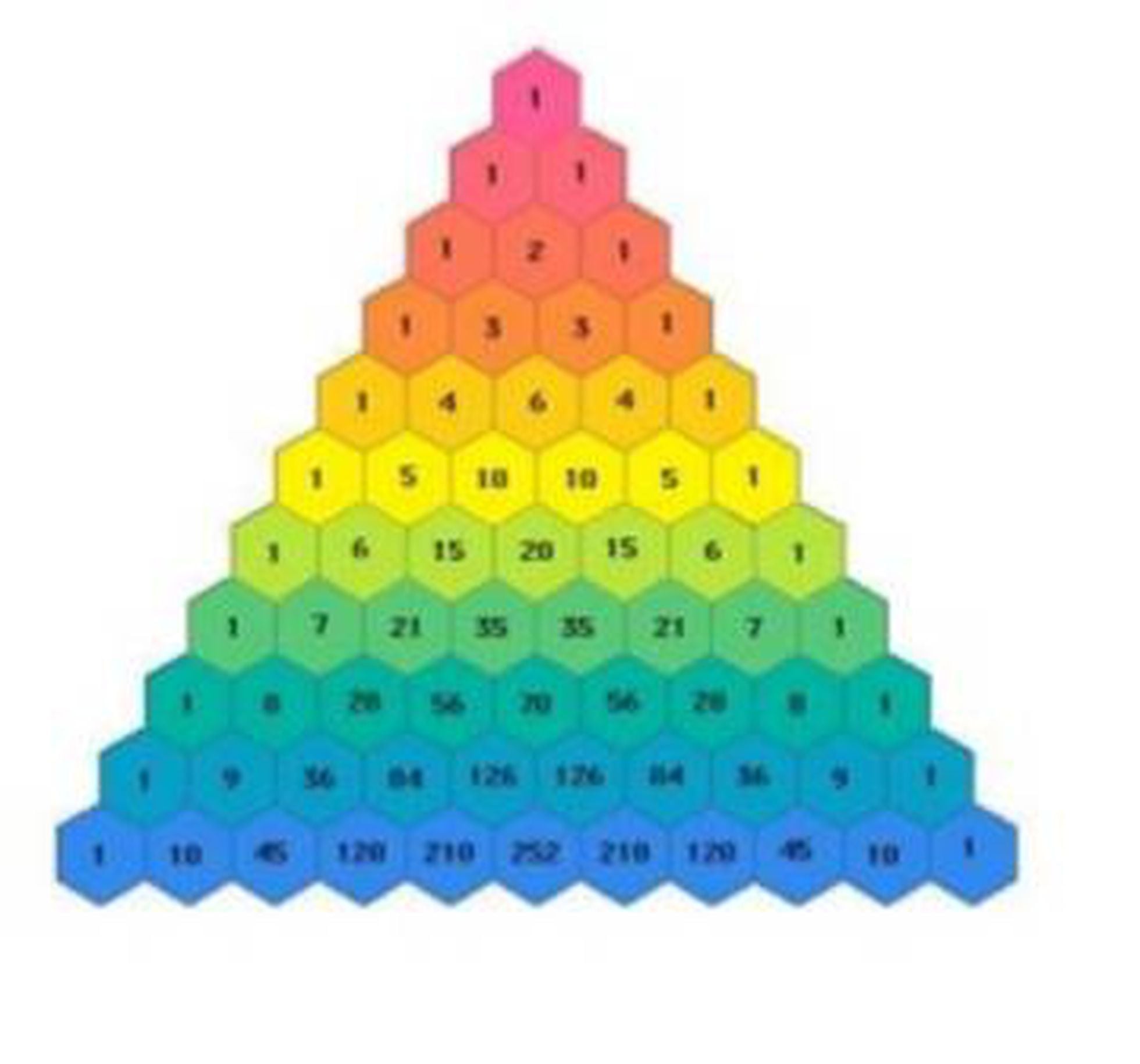
El triángulo de Pascal Ciencia EL PAÍS
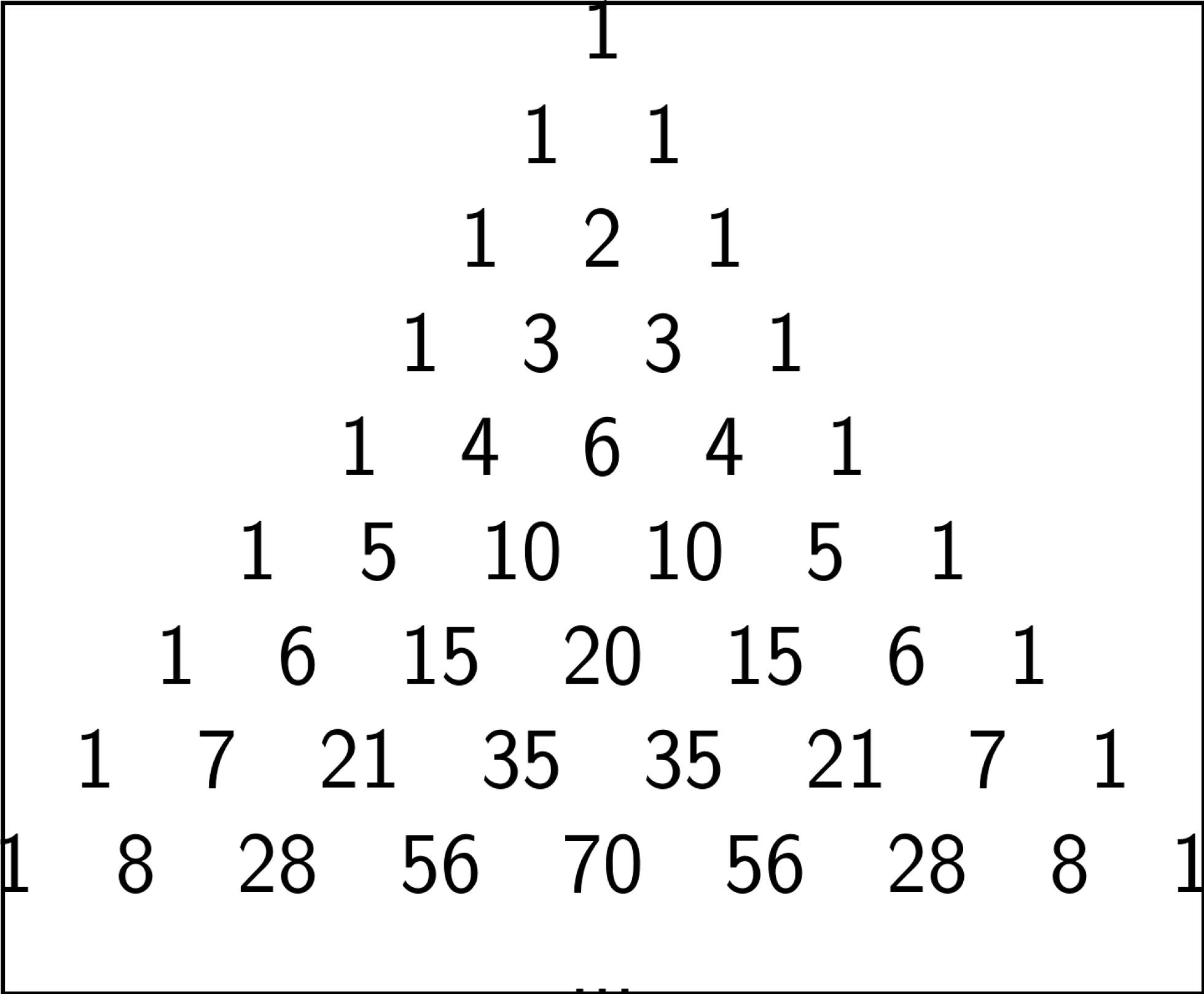
TRABAJO DE TRIANGULO DE PASCAL MATEMÁTICAS Y TRIGONOMETRÍA

Triángulo de Pascal EcuRed

Il triangolo di Tartaglia detto anche triangolo di Pascal YouTube

The 10th dimension of Pascal’s Triangle and consciousness Nexus Newsfeed
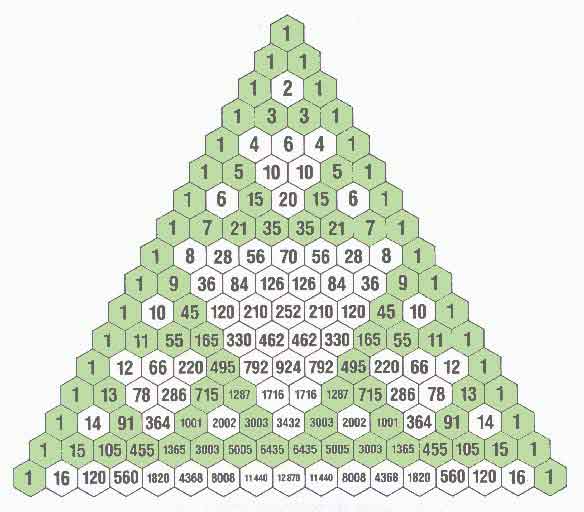
HYPATIA. MATEMÁTICAS El Triángulo de Pascal o de Tartaglia

El Triángulo de Pascal Teoría YouTube
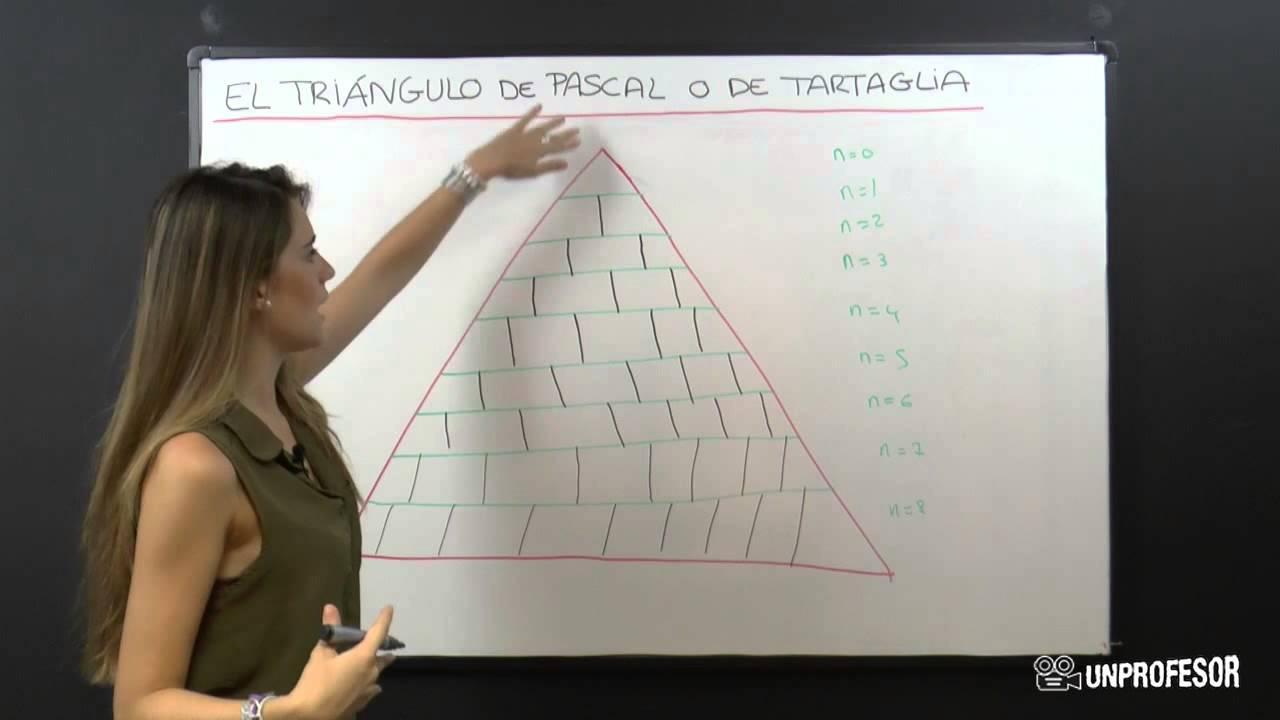
El triángulo de Pascal o de Tartaglia
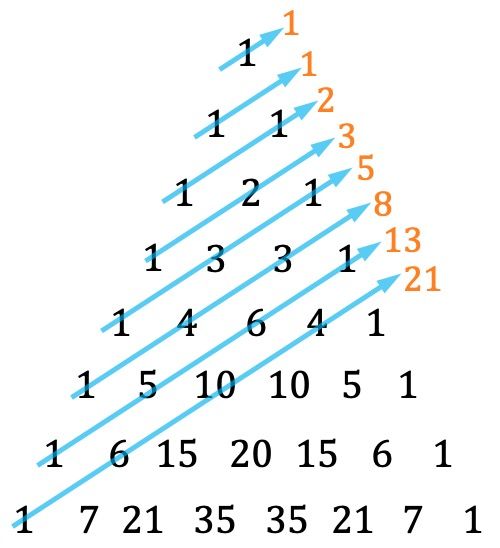
Triángulo de Tartaglia (o triángulo de Pascal)

MATHERS El triángulo de Tartaglia

El triángulo de Pascal o Tartaglia Números Conceptos matemáticos

triangulo de pascal

Triangulo de pascal Triángulo de Pascal El triángulo de Tartaglia también se conoce como

Triángulo de Pascal YouTube
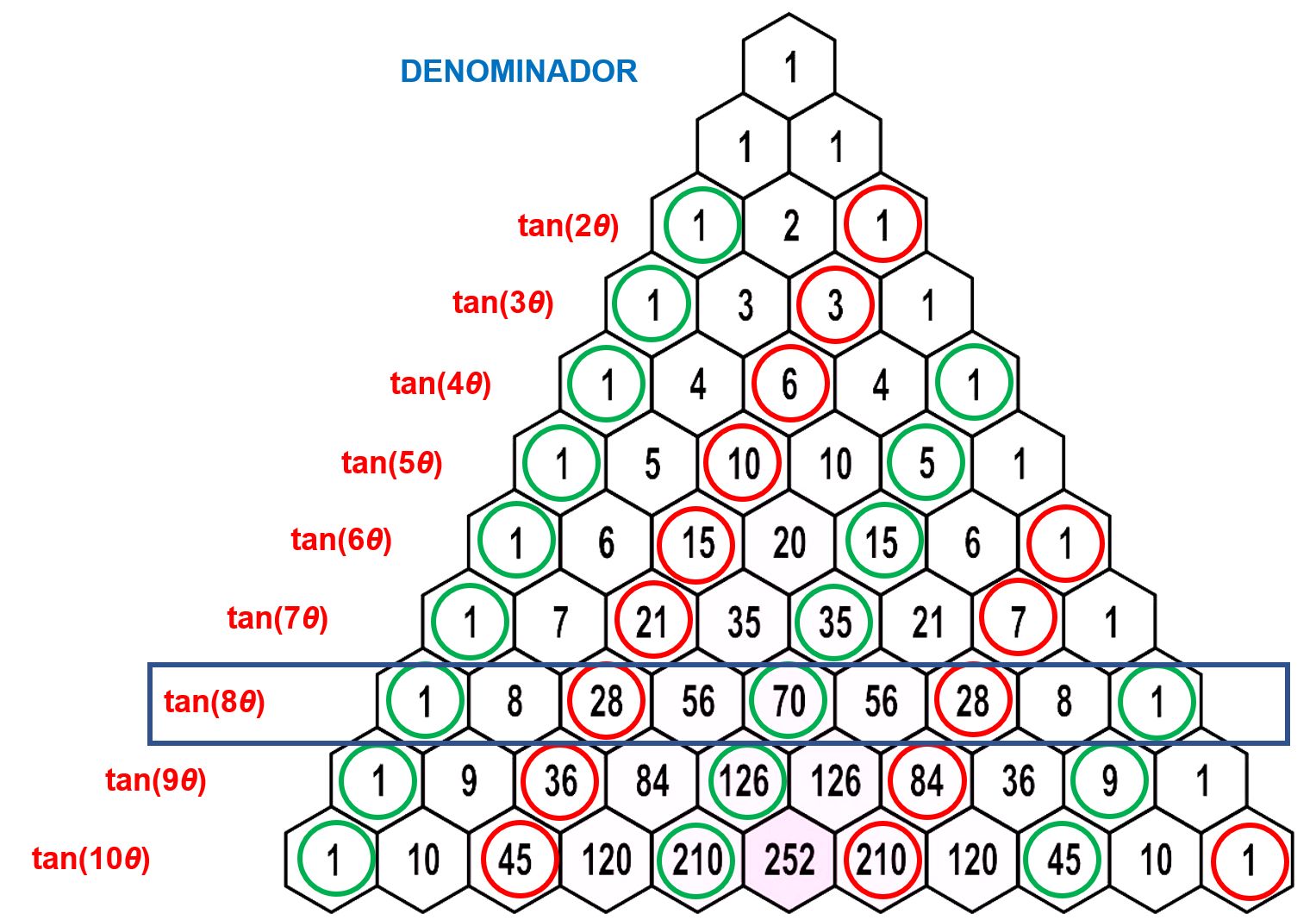
El triángulo de Pascal para calcular tangentes — Cuaderno de Cultura Científica

Binomio de Newton y Triángulo de Pascal o Tartaglia (EJEMPLOS RESUELTOS!!!) YouTube
Una interesante recopilación de algunas de las curiosidades matemáticas que se pueden encontrar en el triángulo de Pascal. Washington Park MAX Station. Foto de Chris Phan. Miguel Ángel Morales.. El triángulo de Pascal es la representación gráfica de los coeficientes binomiales. Estos coeficientes son esenciales en el cálculo de las potencias de un binomio. Cálculo de combinaciones. El número de combinaciones de n elementos tomados de k en k se puede determinar mediante el uso del triángulo de Tartaglia. Sucesión de Fibonacci.